| Picture | Details | Pages | Download |
 |
I. Grebennik, D. Grytsay and S. Shekhovtsov. OPTIMAL PLACEMENT PROBLEM IN PRINTING PRODUCTION
Abstract — In the article we deal with the optimal placement problem in manufacturing printing products. A special set of two-dimensional geometric objects bounded by circular arcs and line segments are introduced as mathematical models of real-life printing objects. We derive phi-functions, as well as normalized and pseudo-normalized phi-functions to describe the relations (non-overlapping, containment and distance constraints) between the geometric objects. A mathematical model of the optimal placement of printing objects is constructed and a solution strategy is proposed. Index Terms – cutting, phi-functions, printing objects, mathematical model, solution strategy. References:
Igor V. Grebennik received Doctor of Technical Sciences degree in Mathematical Modeling and Computational Methods (2007) from Institute for Problems in Machinery of National Academy of Sciences of Ukraine (Kharkov). From 2007 he is a professor at the Department of Systems Engineering, Kharkiv National University of Radio Electronics. His current research interests include mathematical modeling, operational research, combinatorial optimisation, packing and cutting. Sergey B. Shekhovtsov received Candidate of Technical Sciences degree in Mathematical Modeling and Computational Methods (1989) from Kharkov National University of Radioelectronics (Kharkov). From 1994 he is a associate professor at the Department of Applied Mathematics, Kharkov National University of Internal Affairs. His current research interests include mathematical modeling, operational research, computational geometry, optimisation, packing and cutting. |
4-11 | |
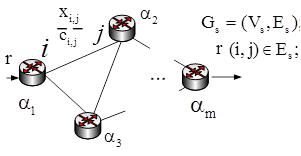 |
SHOSTKO I.S., KULIA YE. APPLICATIONS OF MULTIPATH ROUTING FOR ENERGY BALANCING IN SENSOR NETWORKS
Abstract — When designing a wireless sensor network (WSN) with autonomous nodes there emerges an issue how to provide the maximum duration of its life. For this purpose the use of multipath routing with support of the regime of energy balancing nodes is proposed in the article. The model for study of algorithms, multipath routing considering redressing the imbalance of power consumption in WSN transit nodes is developed. Keywords: wireless sensor network, routing, power, imbalance. References:
Shostko Igor Svetoslavovich, Professor, Doctor of Technical Sciences, Associate Professor, Department of telecommunication systems, Kharkov National University of Radio Electronics. Research interests: ultra-wideband signals in radio engineering and telecommunication systems. Address: Kharkov, Lenin av, 14, Department of TCS, KNURE. Phone: (057) 702-13-20, Е-mail: igor-shostko@yandex.ru Kulia Julia Eduardovna, PhD student, Department of Telecommunication systems, Kharkov National University of Radio Electronics. Research interests: wireless sensor networks, telecommunication systems. Address: Kharkov, Lenin av, 14, Department of TCS, KNURE. Phone: 063-47-22-773, е-mail: sosedka.27@mail.ru |
12-16 | |
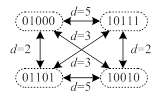 |
VALERY SAPOZHNIKOV, VLADIMIR SAPOZHNIKOV, DMITRY EFANOV, VYACHESLAV DMITRIEV, MARIA CHEREPANOVA. OPTIMUM SUM CODES, THAT EFFECTIVELY DETECT THE ERRORS OF LOW MULTIPLICITIES
Abstract – The article provides the method of formation of the sum code with minimum total number of undetectable errors. The code, suggested by authors, has the same number of check bits, as a classic Berger code, but also has a better detection ability, particularly within the area of low multiplicity errors in data vectors. New sum code allows to develop concurrent error detection (CED) systems of logic units of automation and computer devices with low equipment redundancy and a high percentage of error detection in controlled blocks. References: [1] E.S. Sogomonyan, and E.V. Slabakov “Self-Checking Devices and Fault-Tolerant Systems” (in Russ.), Moscow: Radio & Communication, 1989, 208 p. [2] S.J. Piestrak “Design of Self-Testing Checkers for Unidirectional Error Detecting Codes”, Wrocław: Oficyna Wydawnicza Politechniki Wrocłavskiej, 1995, 111 p. [3] Y.-Y. Guo, J.-C. Lo, and C. Metra “Fast and Area-Time Efficient Berger Code Checkers”, Workshop on Defect and Fault-Tolerance in VLSI Systems, 1997, October 20-22, pp. 110-118. [4] A.Yu. Matrosova, I. Levin, and S.A. Ostanin “Self-Checking Synchronous FSM Network Design with Low Overhead”, VLSI Design. – 2000. – Vol. 11. – Issue 1. – Pp. 47-58. [5] A. Matrosova, I. Levin, and S. Ostanin “Survivable Self-Checking Sequential Circuits”, Proc. of 2001 IEEE International Symposium on Defect and Fault Tolerance in VLSI Systems (DFT 2001), Oct. 24-26, San Francisco, CA, 2001, 395-402 pp. [6] L-T. Wang, C.E. Stroud, and N.A. Touba “System-on-Chip Test Architectures: Nanometer Design for Testability”, Morgan Kaufmann Publishers, 2008, 856 p. [7] R. Ubar, J. Raik, and H.-T. Vierhaus “Design and Test Technology for Dependable Systems-on-Chip (Premier Reference Source)”, Information Science Reference, Hershey – New York, IGI Global, 2011, 578 p. [8] A.H. Abdulhadi, and A.H. Maamar “Self Checking Register File Using Berger Code”, 6th WSEAS International Conference on Circuits, Systems, Control & Signal Processing, 2007, Cairo, Egypt, December 29-31, pp. 62-68. [9] P. Srihari “Sum Codes: A Binary Channel Coding Scheme”, International Journal of Computer Science And Technology, 2014, Vol. 5, Issue 1, pp. 60-64. [10] N.K. Jha, and S. Wang “Design and Synthesis of Self-Checking VLSI Circuits”, IEEE Trans. Computer-Aided Design, 1993, Vol. 12, Issue 6, pp. 878-887. [11] S.S. Gorshe, and B. Bose “A Self-Checking ALU Design with Efficient Codes”, Proceedings of 14th VLSI Test Symposium, Princeton, NJ, USA, 1996, pp. 157-161. [12] M. Nicolaidis, and Y. Zorian “On-Line Testing for VLSI – А Compendium of Approaches”, Journal of Electronic Testing: Theory and Applications, 1998, vol. 12, issue 1-2, pp. 7-20. [13] O. Potin, Ch. Dufaza, and Ch. Landrault “A New Scheme for Off-Line and On-Line Testing With ABC And Berger Encoding”, Proc. 4th IEEE Int. On-line Testing Workshop, Italia, Capri, 1998, 71-75. [14] D. Das, and N.A. Touba “Weight-Based Codes and Their Application to Concurrent Error Detection of Multilevel Circuits”, Proc. 17th IEEE Test Symposium, USA, California, 1999, pp. 370-376. [15] V.V. Sapozhnikov, and Vl.V. Sapozhnikov “Self-Checking Discrete Devices” (in Russ.), St. Petersburg: Energoatomizdat, 1992, pp. 224. [16] L.D. Cheremisinova “Logical Synthesis of Combinational KMOP Circuits Considering the Power Dissipation” (in Russ.), Bulletin of Tomsk State University. Management, Computer Engineering and Informatics, 2014, Issue 3, pp. 89-98. [17] P.P. Parkhomenko, and E.S. Sogomonyan “Basics of Technical Diagnostics (Optimization of Diagnostic Algorithms and Equipment)” (in Russ.), Moscow: Energoatomizdat, 1981, pp. 320. [18] J.M. Berger “A Note on Error Detection Codes for Asymmetric Channels”, Information and Control, 1961, vol. 4, issue 1, pp. 68-73. [19] D.V. Efanov, V.V. Sapozhnikov, and Vl.V. Sapozhnikov “On Sum Code Properties in Functional Control Circuits”, Automation and Remote Control, 2010, vol. 71, issue 6, pp. 1117-1123. [20] A.A. Blyudov, D.V. Efanov, V.V. Sapozhnikov, and Vl.V. Sapozhnikov “Formation of the Berger Modified Code with Minimum Number of Undetectable Errors of Informational Bits” (in Russ.)”, Electronic Modeling, 2012, vol. 34, issue 6, pp. 17-29. [21] A.A. Blyudov, D.V. Efanov, V.V. Sapozhnikov, and Vl.V. Sapozhnikov “Sum codes for organization of control of combinational circuits”, Automation and Remote Control, 2013, vol. 74, issue 6, pp. 1020-1028. [22] D. Efanov, V. Sapozhnikov, Vl. Sapozhnikov, and A. Blyudov “On the Problem of Selection of Sum Code for Combinational Circuit Test Organization”, Proceedings of 11th IEEE East-West Design & Test Symposium (EWDTS`2013), Rostov-on-Don, Russia, September 27-30, 2013, pp. 261-266. [23] A.A. Blyudov, D.V. Efanov, V.V. Sapozhnikov, and Vl.V. Sapozhnikov “On Codes with Summation of Unit Bits In Concurrent Error Detection Systems”, Automation and Remote Control, 2014, vol. 75, issue 8, pp. 1460-1470. [24] V.V. Saposhnikov, and Vl.V. Saposhnikov “New Code for Fault Detection in Logic Circuits”, Proc. 4th Int. Conf. on Unconventional Electromechanical and Electrical Systems, St. Petersburg, Russia, June 21-24, 1999, pp. 693-696. [25] V. Mehov, V. Saposhnikov, Vl. Sapozhnikov, and D. Urganskov “Concurrent Error Detection Based on New Code with Modulo Weighted Transitions between Information Bits”, Proc. of 7th IEEE East-West Design&Test Workshop (EWDTW`2007), Erevan, Armenia, September 25-30, 2007, pp. 21-26. [26] V.B. Mekhov, V.V. Saposhnikov, and Vl.V. Saposhnikov “Checking of Combinational Circuits Basing on Modification Sum Codes”, Automation and Remote Control, 2008, vol. 69, issue 8, pp. 1411-1422. [27] V.V. Sapozhnikov, Vl.V. Sapozhnikov, D.V. Efanov, and V.V. Dmitriev “Properties Of Sum Codes With Weighted Transitions With Direct Sequence Of Weight Ratios (in Russ.)”, Computer Science and Control Systems, 2014, issue 4, pp. 77-88. Valery Sapozhnikov is with the Petersburg State Transport University, Automation and Remote Control on Railways Department, Russian Federation. Vladimir Sapozhnikov is with the Petersburg State Transport University, Automation and Remote Control on Railways Department, RF. Dmitry Efanov is with the Petersburg State Transport University, Automation and Remote Control on Railways Department, RF (corresponding author to provide e-mail: mitriche@yandex.ru). Vyacheslav Dmitriev is with the Petersburg State Transport University, Automation and Remote Control on Railways Department, RF. Maria Cherepanova is with the Petersburg State Transport University, Automation and Remote Control on Railways Department, RF. |
17-22 | |
 |
CHERNYSHOV N.N. CONDUCTIVITY OF MULTI-COMPONENT ELECTRON GAS
Abstract - The 2D semimetal consisting of heavy holes and light electrons is studied. The consideration is based on the assumption that electrons are quantized by magnetic field while holes remain classical. We assume also that the interaction between components is weak and the conversion between components is absent. The kinetic equation for holes colliding with quantized electrons is utilized. It has been stated that the inter-component friction and corresponding correction to the dissipative conductivity σxx do not vanish at zero temperature due to degeneracy of the Landau levels. This correction arises when the Fermi level crosses the Landau level. The limits of kinetic equation applicability were found. We also study the situation of kinetic memory when particles repeatedly return to their meeting points. Key words: electron system, magnetic field, limit, kine-tic equation, oscillator and distribution function. References: [1] Blokh M.D., Magarill L.I. Theory of photogalvanic effect on free carriers // PTG, vol. 22, №8, 1980, pp. 2279-2284 (in Russian). [2] Chernyshov N.N. Theory of transfer phenomena in an electric field for crystals without an inversion centre // Physical surface engineering, vol. 10, №1, NPTC, Kharkov, 2012, pp. 96-101 (in Russian). [3] Chernyshov N.N. Photogalvanic effect in crystals without a centre of inversion in view of electron-hole interaction /All- Ukrainian collected volume // Radiotechnika, № 177, KhNURE, 2014, pp. 94-97. (in Russian) [4] Chernyshov N.N., Slipchenko N.I., Tsymbal A.M., Umyarov K.T, Lukianenko V.L. The photogalvanic effect within spin resonance in quantizing magnetic field // Physical surface engineering, vol. 11, №4, NPTC, Kharkov, 2013, pp. 427-430. [5] Chern Y.F., Dobrovolska M., et al. Interference of electric-dipole and magnetic-dipole interactions in conduction-electron-spin resonance in InSb // Phys. Rev. B., vol. 32, 1985, pp. 890-902. [6] Gantmakher V.F., Levinson Y. B.. Sov. Phys. // JETP 47, 1978, 133 p. [7] Adams E.N., Holstein T.D.. J. Phys. Chem. Solids 10, 1959, 254 p. [8] Ando T., Uemura Y.. J. Phys. Soc. Jpn 36, 1974, 959 p. [9] Baskin E.M., L.I. Magarill. Sov. Phys. // JETP 48, 1978, 365 p. [10] Fogler M., Perel V., B. Shklovskii, Phys. Rev. B 56, 1997, 6823 p. Nikolay Chernyshov is with the Kharkov National University of Radio Electronics, Department of Microelectronics and Electronic Valves and Devices, Ukraine, e-mail: chernyshov@kture.kharkov.ua |
23-25 | |
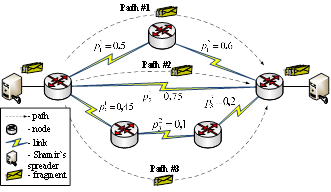 |
OLEKSANDRA S. YEREMENKO, ALI SALEM ALI. SECURE MULTIPATH ROUTING ALGORITHM WITH OPTIMAL BALANCING MESSAGE FRAGMENTS IN MANET
Abstract — This paper is devoted to the proposition of the algorithm of secure multipath routing with optimal balancing message fragments number in MANET. The work considered the concept of the threshold secret sharing scheme in relation to secure routing using non-overlapping paths for the message fragments transmission. Based on the analysis of disadvantages of existing mechanism SPREAD, it was proposed to improve the fragments allocation model, which had been reduced to the optimal balancing of message fragments number transmitted over the non-overlapping paths. Several optimality criteria were suggested as to the solution of balancing problem using Shamir`s scheme with or without redundancy. In the comparative analysis it was justified to use optimality criterion in practice, providing, on the one hand, minimization of dynamically managed upper bound number of fragments transmitted over separate non-overlapping paths in the network, and on the other hand –adaptation to security parameters (probability of compromise) of individual network elements: nodes, links and paths. Numerical examples of models with different optimality criteria of the solutions obtained, and their comparative analysis were presented. Within the proposed algorithm it is suggested to use the model under which the minimum number of fragments is transmitted by the worst path in terms of the probability of compromise, whereas their maximum number - by the best path. Keywords — Secure routing, MANET, probability of compromise, number of fragments balancing, non-overlapping paths. References:
Oleksandra S. Yeremenko received her Ph.D. in Telecommunication Systems and Networks from the Kharkiv National University of Radio Electronics (2008) and academic rank of Senior Researcher (2012). She joined the Department of Telecommunication Systems at the Kharkiv National University of Radio Electronics as a senior research assistant in 2007. She has been an associate professor of the Department of Telecommunication Systems since 2011. Her current research interests are NGN, TCP/IP, Network Security, and Fault-Tolerant Routing. Ali Salem Ali received his B.Sc. in Computer Science from the Al-ma`amoon University, Baghdad, Iraq (2005) and M.Sc. from the National Technical University Kharkiv Polytechnic Institute (2008). He received his Ph.D. in Telecommunication Systems and Networks from the Kharkiv National University of Radio Electronics (2012). He joined the Network Engineering Department at the Al Iraqi University (Iraq, Baghdad, Adhamiya) as a Teacher in 2012. His current research interests are in the area of Network Protocols and Routing. |
26-29 | |
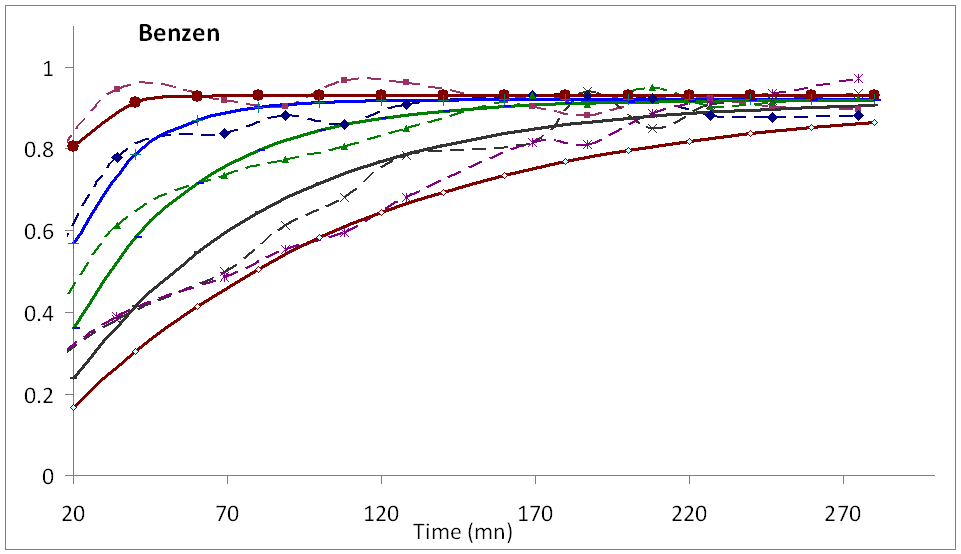 |
PETRYK M. PARAMETER IDENTIFICATION OF COMPETITIVE DIFFUSION OF NANOPOROUS PARTICLES MEDIA USING GRADIENT METHOD AND THE HEVISIDE’S OPERATIONAL METHOD
Abstract – The identification of competitive diffusion parameters in heterogeneous nanoporous materials is analyzed. Solutions to the direct and inverse problems are basing on the Heaviside’s operational method and gradient method are obtained. New procedures for identification of diffusion coefficients for co-diffusing components (benzene and hexane) in intra- and intercrystallite spaces are implemented using high-speed gradient methods and mathematical diffusion models as well as the NMR spectra of the adsorbed mass distribution of each component in the zeolite bed. The gradient of the residual functional is obtained basing on optimal control theory. These diffusion coefficients are obtained as a function of time for different positions along the bed. Benzene and hexane concentrations in the inter- and intracrystallite spaces for every position in the bed and for different adsorption times are calculated. Key words: mathematical model, competitive diffusion, direct end inverse boundary problems, functional identification, gradient method, Heviside’s operational method, nanoporous media. References: [1] M. Fernandez, J. Kärger, D. Freude, A. Pampel, J.M. van Baten, R. Krishna, Microporous and Mesoporous Materials 105 (2007) 124-131. [2] L.F. Gladen, M.D. Mantle, A.J. Sederman, Handbook of Heterogeneous Catalysis, 2nd Edition Eds: G. Ertl, H. Knözinger, F. Schüth, J. Weitkamp, Wiley-VCH, Weinheim 2008. 1784 P. [3] A. A. Lysova, I. V. Koptyu, Chem. Soc. Rev. 39 (2010) 4585-4601. [4] P. N’Gokoli-Kekele, M.-A. Springuel, J.-J. Bonardet, J.-M. Dereppe, J. Fraissard, Studies in Surface Science and Catalysis 133 (2001) 375-382. [5] S. Leclerc, G. Trausch, B. Cordier, D. Grandclaude, A. Retournard, J. Fraissard, D. Canet, Magn. Reson. Chem. 44 (2006) 311- 317. [6] M. Petryk, S. Leclerc, D. Canet, J. Fraissard, Diffusion Fundamentals 4 (2007) 11.1. Online in http://www.diffusion-fundamentals.org [7] M. Petryk, S. Leclerc, D. Canet, J. Fraissard, Catalysis Today 139 (2008) 234-240. [8] S. Leclerc, M. Petryk, D. Canet, J. Fraissard, Catalysis Today 187 (2012) 104-107. [10] C. Fërste, A. Germanus, J. Curger, H. Pfeifer, J. Caro, W. Pilz, A. Zikanova, J. Chem. Eng. Soc., Faraday Trans. 1 83 (1987) 2301-2309. [11] R. Krishna, J.M. van Baten, Chem. Eng. Journal 140 (2008) 614-620. [12] A.N. Tikhonov and V.Y. Arsenin. Solutions of Ill-Posed Problems, Washington D.C. : V.H. Winston ; New York : J. Wiley (1977), 288 P. [13] J.-L. Lions, Perturbations Singulières dans les Problemes aux Limites et en Contrôle Optimal, New York: Springer. Lecture Notes in Math. Ser. 2008 645 P. [14] O.M. Alifanov, Inverse problems of heat exchange, Moscow: Engineering (1988) 280 P. [15] V. Deineka, M. Petryk, J. Fraissard, Cybernetics and System Analysis, Springer 47(5) (2011) 705-723. [16] M. Petryk, J. Fraissard, J. of Automation and Information Sciences 41(3) (2009) 37-55. [17] I.V. Sergienko, V.S. Deineka, Optimal Control of Distributed Systems with Conjugation Conditions, New York: Kluwer Aсademic Publishers (2005) 400 P. Petryk Mykhaylo, Dr of Sc., Prof., is with the Ternopil National Technical University named after Ivan Pulu’y. Address: 56 rue Ruska, 46001 Ternopil, Tél. 38 035 2 25 64 96; Fax 380352254983, e-mail: Mykhaylo_Petryk@tu.edu.te.ua; SoftEng@utc.fr |
30-36 | |
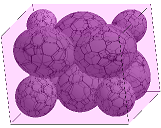 |
PANKRATOV A., ROMANOVA T., KHLUD O. QUASI-PHI-FUNCTIONS IN PACKING PROBLEM OF ELLIPSOIDS
Abstract - The paper considers the problem of packing a given collection of ellipsoids of revolution into a rectangular container of minimal volume. Our ellipsoids can be continuos rotated and translated. A class of radical-free quasi-phi-functions is used for an analytical description of non-overlapping and containment constraints. We formulate the packing problem in the form of a nonlinear programming problem and propose a solution strategy, which allow us to search for local optimal packings. The actual search for a local minimum is performed by IPOPT. We provide computational results. Index Terms – packing, ellipsoids, continuous rotations, non-overlapping, containment, quasi-phi-functions, solution algorithm, nonlinear optimization References:
Alexandr V. Pankratov received Doctor of Technical Sciences degree in Mathematical Modeling and Computational Methods (2013) from Institute for Problems in Machinery of National Academy of Sciences of Ukraine (Kharkov). From 2013 he is a senior researcher at the Department of Mathematical Modeling and Optimal Design, Institute for Mechanical Engineering Problems of the National Academy of Sciences of Ukraine. His current research interests include mathematical modeling, operational research, computational geometry, optimisation, packing, cutting and covering. Tatiana E. Romanova received Doctor of Technical Sciences degree in Mathematical Modeling and Computational Methods (2003) from Institute of Cybernetics of the National Academy of Sciences of Ukraine (Kiev). From 2002 he is a senior researcher at the Department of Mathematical Modeling and Optimal Design, Institute for Mechanical Engineering Problems of the National Academy of Sciences of Ukraine. From 2005 she is a professor at the Department of Applied Mathematics, Kharkiv National University of Radioelectronics. Her current research interests include mathematical modeling, operational research, computational geometry, optimisation, packing, cutting and covering. Olga M. Khlud received Bachelor's degree in System Analysis (2014) from Kharkiv National University of Radioelectronics. She is an undergraduate at the Kharkiv National University of Radioelectronics. Her current research interests include mathematical modeling, operational research, packing and cutting. |
37-41 |